Follow the Energy from the Sun to Earth

Mean air temperature just above Earth’s surface is determined primarily by the net radiant solar energy absorbed by the Earth-atmosphere system minus the net energy lost to space by the Earth-atmosphere system through radiation, evapotranspiration and thermal air currents. Global climate change results from a change in at least one of these flows of thermal energy that persists for years. To understand global warming, we need to follow the energy.

Energy exists in many forms (Coopersmith, 2010), but the universal attribute of energy is that it is the agent of change. Energy causes change; change dissipates energy. “In any natural process there exists an inherent tendency towards the dissipation of useful energy” (Wikipedia: Entropy). Without change there could be no concept of time because there would be no way to observe time. Energy is dissipated over time; time runs in the direction of the dissipation of energy. Over time, enthalpy is dissipated, entropy is increased. Also the rate that change can occur decreases as energy decreases. Temperature is the macroscopic measure of the amount of microscopic, very high frequency, oscillatory energy contained within matter. Rates of change decrease toward zero as temperatures decrease toward absolute zero.

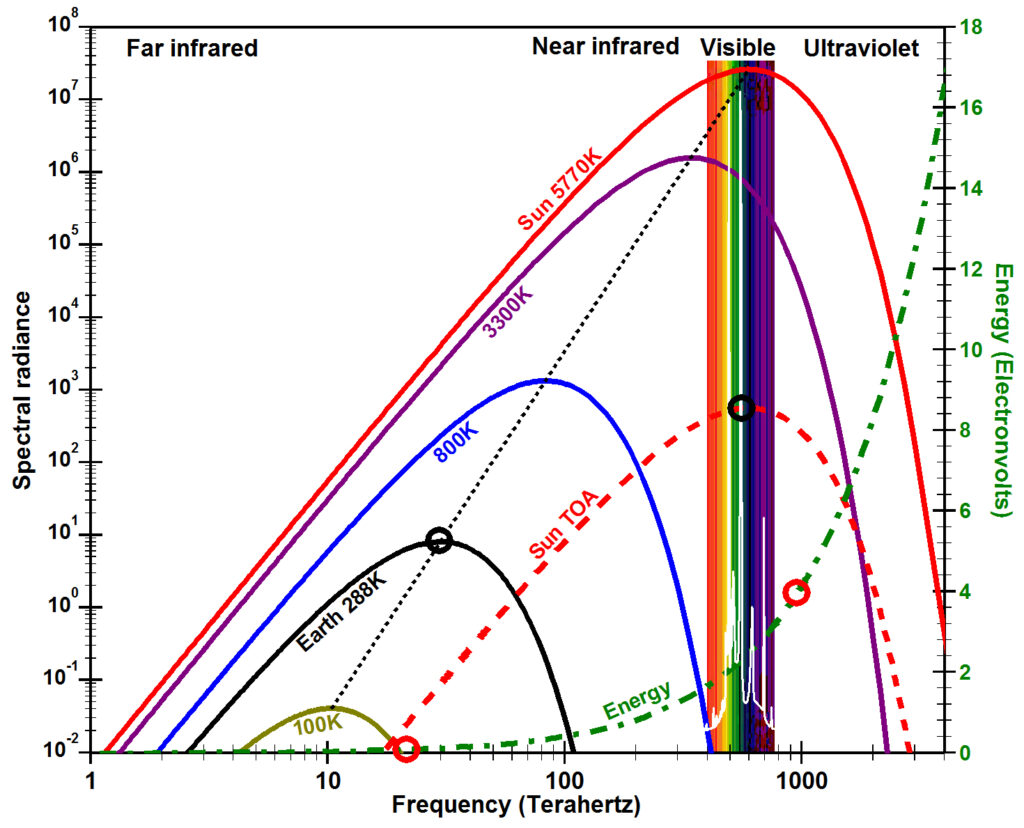
Spectral radiance, temperature, and energy

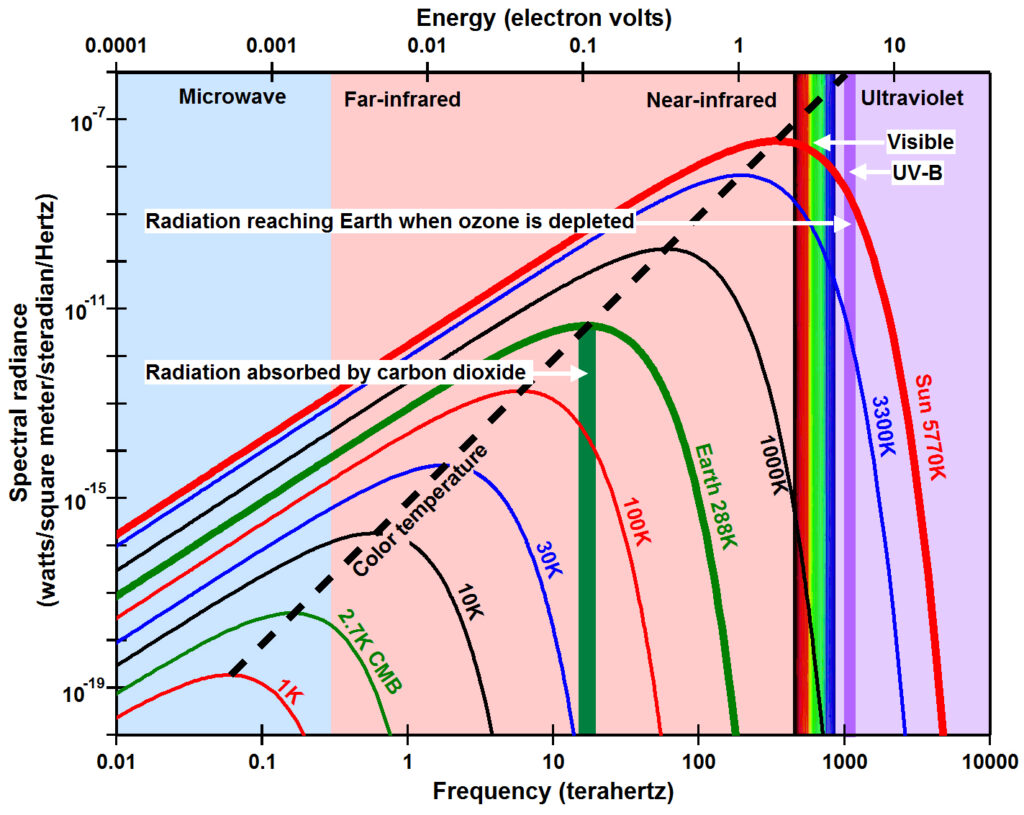
In 1900, Max Planck derived a mathematical expression that accurately approximates the observed spectral radiance emitted by a black body at thermodynamic equilibrium as a function of the temperature of the surface emitting the electromagnetic radiation. Radiance in watts is the total energy in joules of radiation emitted per second within a given solid angle onto a square meter of surface area perpendicular to the radiant ray. Spectral radiance is the amount of radiance at each frequency. A black body is a body of matter that is assumed to be a perfect absorber and emitter of electromagnetic radiation. The values of this equation, now known as Planck’s law, are plotted in the figure for surface temperatures typical for the Sun at 5770K (Kelvin) (red line), Earth at 288K (black), the filament of a typical incandescent light bulb at 3300K (purple), and two intermediate temperatures 800K (blue) and 100K (olive). The frequency of the peak spectral radiance for a black body can be calculated using Wien’s displacement law as 5.88 x 10¹⁰ times the temperature T in Kelvin (dotted black line).

Temperature is an intensive physical property of a body of matter, which means it is independent of how much matter is present. Temperature, as we experience it, is only meaningful when the microscopic oscillatory energy is integrated over a very broad spectral band described by Planck’s law from the very highest frequencies to the very lowest frequencies at which the chemical bonds holding matter together can oscillate given their dimensions and other physical properties. Observations show that this integration is done in Nature via the physical (mechanical) contacts between the components of matter. These oscillations occurring at many frequencies that vary in amount (intensity, brightness) become homogenized through the flow of thermal energy via conduction, to approach thermal equilibrium where the distribution of frequencies and intensities for radiation emitted by a black body at some temperature is approximated by Planck’s law. Temperature is only defined when the oscillations throughout some volume have reached thermal equilibrium, which means the oscillations and therefore the temperatures have become spatially and temporally uniform.

Heat flows (dissipates) from higher energy to lower energy, from higher amplitude to lower amplitude, from higher temperature to lower temperature. Note in the figure that when temperature is increased, the spectral radiance is increased for each and every frequency and the peak spectral radiance is moved to a higher frequency (to the left). This is the primary reason why a colder black body cannot warm a warmer black body; a colder body does not have enough spectral radiance (amount of oscillation) at each frequency and does not have enough high-frequency oscillations.

To derive his law, Planck had to postulate that the energy (E) contained within electromagnetic radiation is equal to the frequency (ν, the Greek letter Nu) times a constant (h), now known as the Planck constant. E=hν, now known as the Planck postulate or the Planck relation, is plotted above as the dash-dot green line. Note how rapidly the energy increases to the left as frequency increases from the infrared, to the visible, to the ultraviolet bands due to the logarithmic scales of the x-axis and the y-axis. The energy contained in ultraviolet radiation that causes sunburn for humans with a wavelength of 310 nm and an energy of 4.0 electron volts (eV) is 48 times the energy contained in infrared radiation with wavelengths around 14,900 nm (0.0832 eV) absorbed strongly by carbon dioxide (CO₂) (red circles).

Atmospheric chemists are very familiar with the Planck postulate (E=hν), using hν in their equations such as

O₂ + hv (λ<242.4 nm) → O(³P) + O(³P)

which says the chemical bond of an oxygen molecule (O₂) in the presence of solar radiation containing energy (hv) at wavelengths (λ) less than 242.4 nm, which has a frequency greater than 1.24×10¹⁵cycles per second and an energy greater than 5.11 eV, oscillates with high enough energy to overcome the bond energy, forming two oxygen atoms in the ground-level triplet state O(³P). Thus E=hν can be thought of as the energy needed to cause a chemical reaction and the spectral amount can be thought of as the number of oxygen atoms that can be photodissociated.

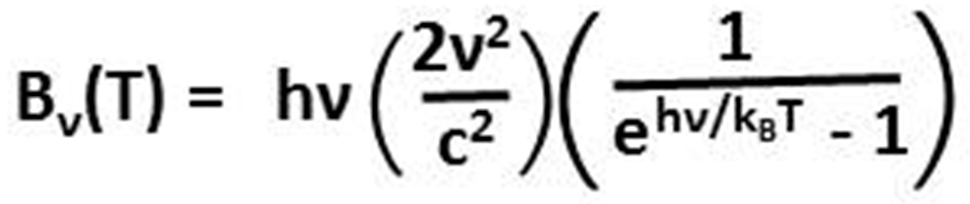
Planck’s law can be written as the energy at each frequency (hν) times the amount of radiation at that frequency as shown to the left. The frequency (ν) and therefore the energy of radiation (hν) is clearly observed not to change while propagating through air and space even over galactic distances except for Doppler effects when the source is moving towards or away relative to the observer. The amount of radiation (the terms in parentheses), what we perceive as brightness, however, is well observed to decrease according to the inverse square law as radiation spreads out from the source. This complete and distinct separation for electromagnetic radiation in space between energy and the amount of energy is counterintuitive because we are used to thinking about the energy of waves in matter where energy is proportional to the square of the amplitude; this energy in matter is the low-frequency energy required to deform matter at macroscopic scales, not the very high-frequency thermal energy contained within matter. Light in the vacuum of space does not travel as a wave in matter nor in any other luminiferous aether.

The difference between temperature as we experience it and high-energy oscillations is well illustrated by the difference in energy radiated by an incandescent light bulb and a fluorescent lamp. The dashed white line on top of the visible spectrum in the figure above right shows radiation from a typical fluorescent lamp in units of counts with the maximum near 4000 counts. Essentially all the radiation is along a few narrow spectral lines generated by a mercury arc and phosphors doped with terbium and europium that fluoresce within the visible spectrum and is essentially all useful as visible light; we perceive the fluorescent lamp as being relatively cool. The purple line, on the other hand, represents radiation from the filament of an incandescent light bulb with a temperature of 3300K isolated by a partial vacuum from the surface of the light bulb. Yet we perceive the bulb as very hot. Most of the energy radiated from the incandescent light bulb is outside of the visible spectrum and perceived as heat. Fluorescent lamps are much more energy efficient than incandescent light bulbs because they produce primarily visible light rather than primarily invisible heat.

Energy in space

According to Planck’s law, the amount of Sun’s peak spectral radiance is 2.6 x 10⁷ watts per steradian per square meter per cycle per second (W sr^-1 m^-2 Hz^-1) at a wavelength of 480 nanometers (nm) in the blue part of the visible spectrum for a solar surface temperature of 5770K (Harder et al., 2009). The amount of peak radiation that reaches the top of Earth’s atmosphere (Sun TOA, dashed red line) is only 568 W sr^-1 m^-2 Hz^-1 (nearly 45,800 times smaller), which is Sun’s peak spectral radiance times the square of Sun’s radius divided by the square of the distance from the center of Sun to Earth. When integrated across the appropriate solid angle and all frequencies, this value was observed recently to be between 1361 and 1362 W m^-2 (ACRIM, 2013). The Sun’s peak spectral radiance at the top of the atmosphere (Sun TOA, dashed red line) at 480 nm is 69 times greater than the peak spectral radiance of radiation from Earth (black line) just above Earth’s surface at a wavelength of 10,000 nm (black circles).

Solar energy in space is observed as thermal radiation, an electromagnetic field, the macroscopic manifestation of the very high-frequency oscillations that form an electric field that induces a magnetic field, that induces an electric field ad infinitum. Radiation travels in space at the speed of light, which must be related to the time it takes an electric field to induce a magnetic field, to induce an electric field, ad infinitum. According to Maxwell’s equations , the velocity of light) is equal to the square root of 1/ε_oμ_o where ε_o is the electric constant or vacuum permittivity, the resistance to forming an electric field in a vacuum, and μ_o is the magnetic constant or vacuum permeability, the ability to form a magnetic field in space.Radiation in space does not have a wavelength until it interacts with matter. Radiation in space is simply frequency, which by the Planck postulate is energy. Since radiation cannot be seen until it interacts with matter, radiation in space is dark energy. The existence of dark energy has been proposed from physical cosmological theory. Since Earth receives less than 5×10^-8 % of Sun’s radiation, there must be a lot of dark energy in our solar system that changes in time primarily as the rate of conversion of mass to energy in the Sun changes or changes in space when this energy interacts with matter, such as casting a shadow behind a planet. Warm black bodies radiate thermal energy (heat) according to Planck’s law. Cooler black bodies absorb this thermal energy (heat) and get warmer. I will show below that radiation from cooler black bodies appears to be reflected rather than absorbed by warmer black bodies.

Energy in matter

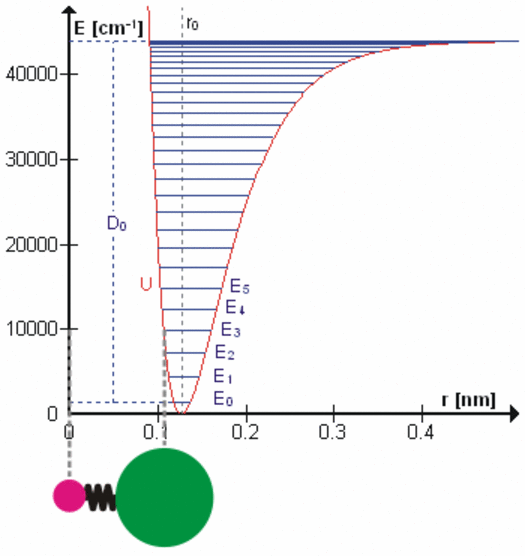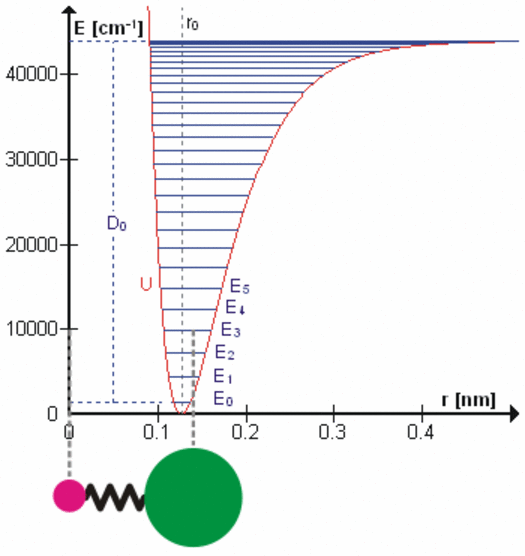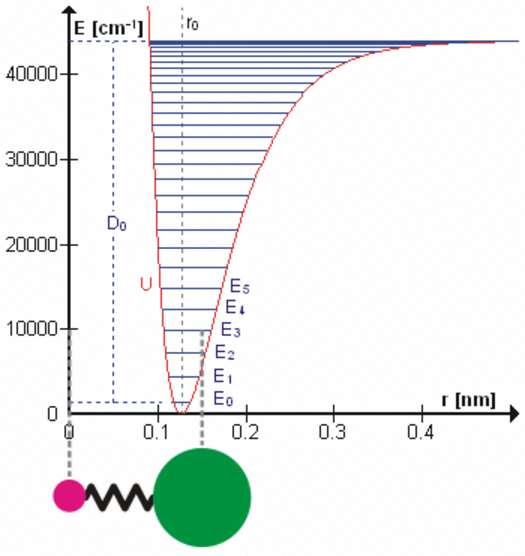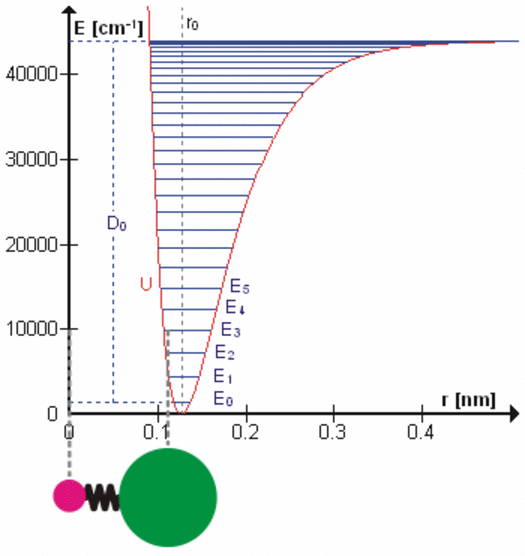
All bonds that hold molecules together are elastic at the atomic level. Each degree of freedom of motion of each molecular bond oscillates about a potential energy minimum between the electrostatic forces that attract atoms and molecules (r > r_o on the right side of the figure to the left) with those that repel atoms and molecules when they get too close (r < r_o). Click on the figure for a more detailed description of the figure and of the various degrees of freedom. These essentially harmonic oscillations are often compared to the oscillations of a mass on a spring shown schematically in the lower left of this figure. These oscillations are at very, very high frequencies ranging from 10¹² to 10¹⁵ cycles per second because the dimensions and masses of the oscillators are so small. When certain gas molecules such as oxygen (O₂) and ozone (O₃) are exposed to solar radiation, D_o in the figure, that is energetic enough, they are photodissociated, meaning the attractive force is no longer strong enough to hold the atoms/molecules together. At even higher energies gases such as nitrogen (N₂) are photoionized, splitting the nitrogen molecule into two nitrogen ions.

At energies less than D_o, each degree of freedom oscillates at frequencies that are the normal modes of a harmonic oscillator determined by the masses and bonding forces of this specific oscillator, much like the fundamental frequency and overtone frequencies of a vibrating string. Each higher frequency is higher energy according to the Planck postulate. A degree of freedom absorbs energy from an electromagnetic field when the amount of oscillation at one of these frequencies in the field is larger than the amount of oscillation at the same frequency in the molecule. Energy is, therefore, transferred via resonance. The fact that the spectral lines of energy absorbed are very narrow shows that this resonance has a very high quality factor (Q factor) meaning a very low rate of energy loss at each resonant frequency. Absorption of energy by resonance also means that energy (heat) can only be transferred from higher amount of energy to lower amount of energy at the same frequency. There are many degrees of freedom for each molecular and atomic bond and each has many normal modes of oscillation so that the detailed nature of the energy transferred from the field to the molecule/atom can be quite complicated as tabulated in spectral databases such as HITRAN. This complicated packet of energy is what we call a photon, a very handy mathematical shorthand for the energy extracted from a radiation field by a molecule or atom.

Resonance is the dominant process in Nature for absorbing or reflecting electromagnetic radiation and for making it visible. When sunlight falls on matter, most of the energy (frequencies) are absorbed. The molecules at the surface that determine color resonate at their natural frequencies emitting radiation only at those frequencies. This is not reflection because the spectral radiance is not a function of the angle of the incoming light. These color frequencies are emitted relatively equally in all directions away from the matter. Wherever your eyeball is, these color rays are focused onto the rods and cones of your eye, which are neurons that resonate at very specific frequencies converting the electromagnetic energy into nerve impulses that your brain associates with a particular color. Every molecule on the surface of the matter does this, but the myriad rays of electromagnetic energy from all the molecules do not interfere with each other and your eye can perceive very detailed differences in color at very high resolution. Similarly lights on a stage can focus beams of light of different colors that pass right through each other and do not interact until they cause matter to resonate.

Your ear works in a similar manner where sound waves in the fluid of the inner ear cause hair cells to resonate. Each hair cell releases a chemical neurotransmitter when stimulated that your brain associates with a given frequency. A common problem for older people is that the hair cells sensitive to high frequency sounds above 1500 cycles per second, lose sensitivity with age making it harder for them to understand what other people are saying.

Absorption of radiant energy by gases

An energy field of radiation in gases is similar to an energy field in space except that certain molecules of a gas can extract narrow spectral bands of energy from the radiation field. Gases do not form black bodies because gases are not perfect absorbers or emitters of radiation. Only some molecules within the gas absorb radiant energy and in the presence of infrared radiation, these molecules only absorb energy along very narrow spectral lines. Also gases do not, in general, have the heat capacity to radiate much energy unless energy is continually being fed to them typically by convection, such as gases forming the radiant surface of the Sun.

When a molecule of carbon dioxide (CO₂), a trace gas, absorbs very small amounts of terrestrial infrared energy, this energy is transferred from the radiant field to the internal oscillatory kinetic energy of the bonds holding the molecule together. But temperature in a gas is observed to be proportional to the average velocity of all molecules and atoms making up the gas, the translational kinetic energy (figure left). Conversion of internal energy to translational energy is assumed to occur during the numerous collisions according to the law of equipartition. The details of this transfer of energy are not clear, but the efficiency is unlikely to be high. When a molecule of oxygen or ozone is photodissociated by ultraviolet radiation, on the other hand, all of the oscillatory kinetic energy that existed in the chemical bond to be dissociated and all of the oscillatory kinetic energy absorbed to dissociate the molecule is converted instantly into translational kinetic energy of the separating molecular pieces, increasing the temperature of the gas very efficiently. The stratosphere is heated primarily by photodissociation of oxygen, ozone, and some other gases.

Absorption of radiant energy by matter

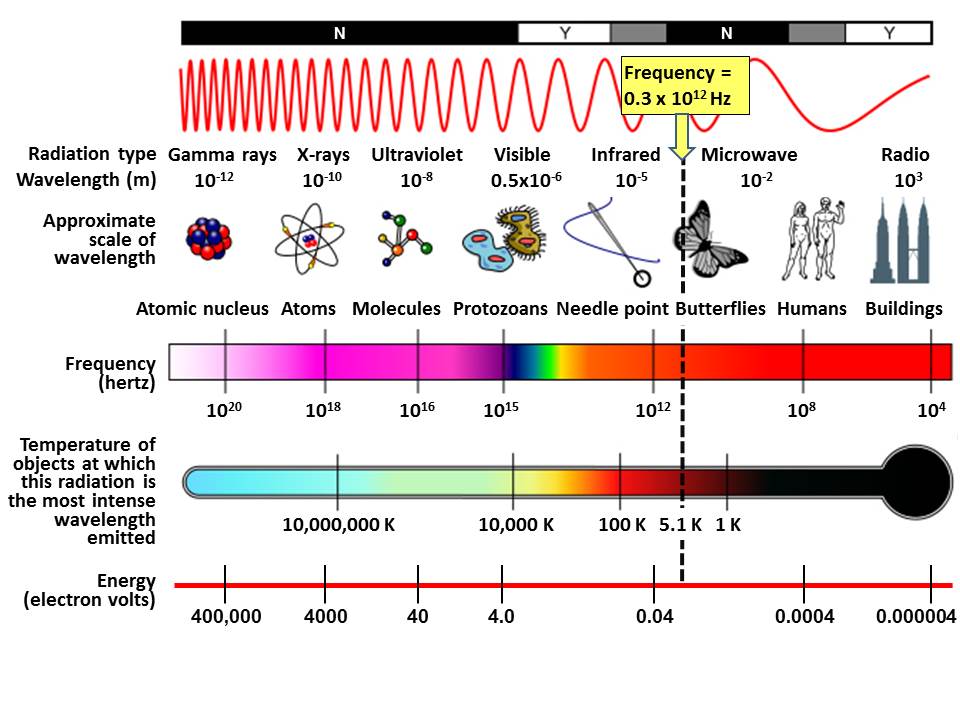
Radiation interacts with matter via resonance. Radiation causes molecules on the surface of matter to oscillate just as specific frequencies of sound in air induce an undamped piano string to vibrate through sympathetic resonance. Molecules on the surface of matter induce their same oscillations in the air or space just above the surface by inducing an oscillating electromagnetic field. The electric frequency produced by a radio transmitter in a radio antenna, for example, induces the same frequency in the surrounding electromagnetic field via resonance. The antenna and electric circuit of a radio receiver tuned to that frequency resonate, extracting energy from the electromagnetic field most efficiently at normal modes of oscillation designed into the radio receiver. The physics is the same for transmission and reception of visible light; only the frequencies and therefore energies involved are nine orders of magnitude larger as shown in the figure above right. Very high-energy, high-frequency radiation such as X-rays and gamma rays, with frequencies well outside of (to left of) Planck curves shown in the figure above right, do not cause resonance in matter, are not absorbed or reflected by matter, and therefore pass straight through matter. The matter is “invisible” or ” dark” when viewed at those very high frequencies.

The Planck postulate (E=hν) and the idea of energy occurring in discrete amounts, published by Planck in 1900, led to Einstein’s light quantum (Einstein, 1905), Lewis’s photon (Lewis, 1926) and both quantum mechanics and quantum electrodynamics, arguably the most successful mathematical theories in physics in terms of explaining and predicting observations. I have carefully outlined a precise description of the microphysics of absorption above to show that you do not need to appeal to quantum mechanics or quantum electrodynamics to understand atmospheric absorption of radiation and transfer of heat. In fact, thinking of electromagnetic radiation in terms of waves or photons in space may be the source of much of the confusion as explained under What is Radiation?. There is no physical evidence for radiant energy traveling as a wave in space until it interacts with matter and the detailed structure of the packet of energy we describe as a photon is determined by the physical details of the molecule absorbing the energy, not by the source of the energy. A photon, therefore, cannot be a packet of energy traveling from the sun; it is the packet of energy extracted by a single molecule from a field of solar radiation. The photon is not a particle as described by the standard model of particle physics. The photon is a very handy mathematical shorthand for a packet of energy whose frequency constituents are rather complex in detail. One can argue that an electron is similarly a standing wave of energy (Dirac, 1927), not a physical particle.

Reflection of radiant energy by matter

When radiation falls on matter, the transfer of energy must also initially be by resonance from the field to the molecules at the surface; from higher amount of oscillation in the field to lower amount of oscillation in the surface of matter. Fourier (1822, p. 33) observed that “every surface which receives rays of heat from surrounding bodies reflects part and admits the rest.” Frequencies with higher spectral amount are absorbed; those with lower spectral amount are reflected. “Reflection of cold, and which, properly speaking, consists in the reflection of too feeble heat” Fourier (1822, p. 38) had been observed by Marc-Auguste Pictet by 1790 and can be observed readily in the laboratory (Evans and Popp, 1985). This is one reason why a layer of air in the atmosphere that is colder than Earth, cannot warm Earth as assumed by greenhouse-gas theory.

Fourier (1822, p. 29) also observed that “the effect of irradiation diminishes as the surface becomes more polished; so that by destroying the polish of the surface, the value of h [the quantity of heat dispersed across a heated surface] is considerably increased.” Polishing a surface increases its specular reflection perhaps by decreasing the average particle size, in effect shortening the antenna length, making molecules on the surface less sensitive to longer-wave radiation. Plus a black surface does not reflect any visible wavelengths and therefore absorbs all wavelengths of radiation, the reason why Planck’s law assumes black bodies.

When radiation falls on matter, the molecules on the surface typically either reflect it or absorb it and pass the absorbed energy on to mechanically touching molecules so that the vibrational energy is shared by conduction, leading to a distribution of frequencies and a temperature shown by Planck’s law once local thermal equilibrium has been reached. The rate at which thermal equilibrium is reached depends on the difference in temperatures, a key property of resonance. As Fourier (1822, p. 456-7) explains: “If two molecules of the same body are extremely near, and are at unequal temperatures, that which is the most heated communicates directly to the other during one instant a certain quantity of heat; which quantity is proportional to the extremely small difference of the temperatures: that is to say, if that difference became double, triple, quadruple, and all other conditions remained the same, the heat communicated would be double, triple, quadruple.”

Penetration of matter by radiant energy

Energy and associated resonance also relate to how readily radiation penetrates matter. Just as a molecule of gas will absorb only those frequencies of radiation that cause resonance based on the physical properties of the degrees of freedom of its molecular bonds, extended matter absorbs only those frequencies of thermal radiation that the matter is already oscillating at. Planck’s law shows the broad range of frequencies absorbed by typical matter as a function of the matter’s temperature. The figure above left shows the values from Planck’s law for the spectral radiance emitted by a black body of matter with temperatures ranging from 5770K for the sun (Harder et al., 2009) to 1K for very, very cold matter in space. The spectral radiance represents the amount of oscillation going on in a body of mass at the given temperature. Thus radiant energy within these frequencies (wavelengths) and with greater spectral amount causes resonance within matter at these temperatures and is therefore absorbed very efficiently.

In general, all matter is oscillating at very low frequencies (long wavelengths and low energy) as shown by the right-sloping part of the Planck curves. Water has many resonant frequencies below the frequencies of visible light: microwaves are readily absorbed, useful for heating water and infrared radiation at most frequencies can barely penetrate the surface of the ocean. Visible light, on the other hand, penetrates meters and ultraviolet radiation penetrates up to tens of meters (Tedetti and Sempéré, 2006). The eyes of some fish have adapted to utilize this ultraviolet energy. The structure of matter also has some effect on what can resonate. For example, infrared radiation is absorbed and reflected by the amorphous (non-crystalline) nature of glass while higher energy, visible radiation penetrates easily. Visible light cannot penetrate the human body but X-rays with energies from 100 eV to 100,000 eV can penetrate humans and many different bodies of matter.

The high frequency, high energy, short wavelength (left) side of the Planck curve is set by chemical reaction or phase transition. The vertical, dashed red lines show the wavelengths of the peak spectral radiance emitted by a black body at the temperature that causes sunburn or the conversion of ice to water or water to water vapor based on Wien’s displacement law. The Planck curves slope rather steeply to the left because chemical reactions or phase transitions are initiated at lower frequencies when the amount of radiation is greater. This is illustrated in the extreme by X-rays. The very high frequency energy of X-rays (3×10¹⁶ Hz to 3×10¹⁹ Hz, energy 100 eV to 100,000 eV) or even ultraviolet rays (7.5×10¹⁴ Hz to 3×10¹⁶ Hz, energy 3.1 eV to 12.4 eV) damages matter. Long exposure to radiant energies above 3.1 eV (ultraviolet wavelengths) cause colors to fade and materials to disintegrate as observed over time with your lawn furniture or house paint. Radiant energies greater than 4 eV (wavelengths <0.31 μm) damage DNA causing sunburn. Since the energies of X-rays exceed 100 eV, the amount or dosage of X-rays used medically must be extremely small in order not to do serious damage. Higher doses of X-rays are often focused on cancer cells in order to kill them. Both the energy and the amount of radiation along the left sloping end of the Planck curve must be high enough to cause a chemical reaction or phase transition.

Molecules of matter oscillate at a broad range of frequencies determined by their temperature. When very high energy radiation, such as X-rays, oscillating at much higher frequencies encounters matter, it causes very little resonance and therefore is hardly absorbed, passing straight through.

Higher frequency radiation just to the left of these curves can also be absorbed, but it causes matter to oscillate at higher than its natural frequencies ultimately causing damage. On Earth (green curve) where temperature averages 288K (15^oC, 59^oF), visible light is absorbed readily causing the molecules responsible for color to resonate so that they emit radiation with that color causing the rods and cones in our eyes to resonate, sending a signal to our brain that we perceive a particular color. But ultraviolet frequencies cause matter to resonate at higher than their normal frequencies ultimately causing damage to DNA, to our skin, to our eyes, to most materials exposed to solar radiation for long periods of time. Much higher-energy radiation such as x-rays, is able to penetrate matter more readily because it is absorbed less efficiently but the dosage must be kept low to prevent chemical reaction leading to damage. In space, dosage is a function of the inverse-square law, it falls in proportion to the square of the distance between source and receiver.

As matter becomes colder and colder, visible radiation appears to be higher and higher energy. the distance along the x-axis in this figure between visible light and the frequencies (wavelengths) of natural oscillations in colder and colder matter becomes greater and greater. This means visible light penetrates matter more readily as the matter gets colder. When we look at empty space, away from suns, stars, planets, etc., we observe very low amounts of thermal radiation in the far infrared to microwave parts of the electromagnetic spectrum. This is known as the cosmic microwave background (CMB) that has a temperature of 2.72548 ±0.00057 K (Fixsen, 2009) (green line). The CMB is thought to be thermal radiation left over from the Big Bang at the origin of the universe, but could simply be thermal radiation from very cold matter that is dark (invisible) because it does not absorb high-energy visible and near-infrared radiation very efficiently. The best way to look for dark matter would be using radiation in the far infrared and microwave parts of the electromagnetic spectrum. But this radiation is very weak. Note in this figure that the peak spectral radiance of the CMB is more than 16 orders of magnitude smaller than peak spectral radiance from the sun and spectral radiance decreases as a function of the square of the distance from source to receiver.

Absorption and loss of radiant energy by Earth

According to Fourier, a body of mass loses heat in two ways: “One is the heat communicated by way of contact to the surrounding air, the other, much less than the first, is the radiant heat emitted.” Fourier (1822, p. 31) “When the heated body is placed in air which is maintained at a sensibly constant temperature, the heat communicated to the air makes the layer of the fluid [air] nearest to the surface of the body lighter; this layer rises more quickly the more intensely it is heated, and is replaced by another mass of cool air. A current is thus established in the air whose direction is vertical, and whose velocity is greater as the temperature of the body is higher” Fourier (1822, p. 30). Most heat from Earth is transferred away by this convective process rather than by radiation as well observed in air currents and weather systems and in the experience of wind chill. Trenberth, Fasullo, and Kiehl (2009), on the other hand, using greenhouse gas theory, calculate that 80% of the energy leaving Earth is by radiation, something that does not appear to be physically possible. This is why they have to assume 68% is radiated back to Earth, which I have just shown is physically impossible. Earth is cooled primarily by convection of heat in the troposphere establishing the environmental lapse rate, the rate that temperature decreases with increasing altitude.

The specific heat capacity of the ocean is much larger than the heat capacity of air. Only 3.2 meters of water in oceans covering 71% of Earth’s surface holds as much heat as the entire atmosphere, and the average depth of the ocean (3682 meters) is more than a thousand times greater. Long-term climate change is more about the change in ocean heat content than about changes in mean surface temperature. According to Levitus et al. (2012), the oceans account for 93% of the warming of the Earth system occurring since 1955.

When radiant energy is absorbed on land during the day, it is not conducted much below the surface of most rocks and other materials. Therefore at night, most of this energy is radiated back into the atmosphere, shown most clearly by warm rocks in a desert environment. At sea, however, visible and especially ultraviolet solar radiation penetrates many meters below the surface (Tedetti and Sempéré, 2006). Plus wave-breaking action, wind-driven currents, and changes in salinity disperse the energy throughout the mixed layer so that radiation into the atmosphere at night is based on the average temperature of the mixed layer that changes primarily with the seasons.

The thermal energy balance of Earth

The mean surface temperature on Earth is determined by a dynamic equilibrium resulting from Earth’s radiation balance between mean thermal energy received at the top of the atmosphere from the Sun and mean thermal energy radiated back into space from the Earth-atmosphere system. Simple calculations (Jacob, 1999, Section 7.2.2) assuming an observed mean albedo of 0.28, meaning that 28% of solar radiation is reflected back into space by clouds and matter on Earth, suggest that mean surface temperature should be around 255K (-18^oC, -0.4^oF). But observed mean temperature is closer to 288K (15^oC, 59^oF). It has been assumed by most scientists that this 33^oC temperature difference is caused primarily by greenhouse gases absorbing infrared thermal radiation emitted by Earth, heating the atmosphere, which then radiates back part of this heat to Earth, warming Earth.

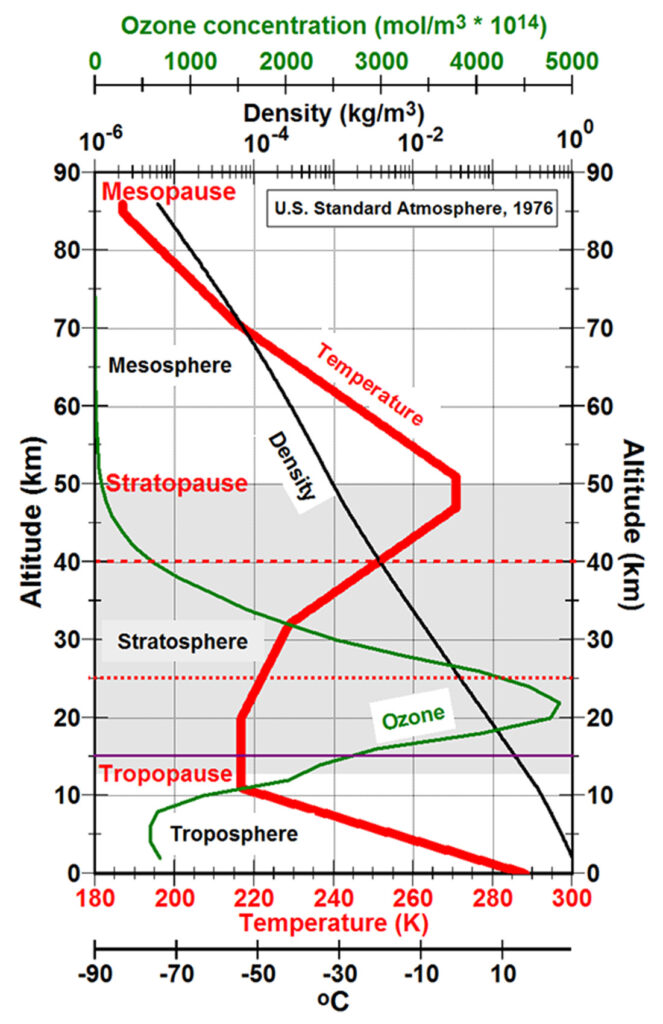
But 255K is the temperature of the radiative surface of the Earth-atmosphere system as seen from space, which should be the temperature of the warmest atmospheric “layer” visible from space, which is the stratopause at an altitude of around 50 km, the thermal lid to the Earth-atmosphere system. The figure to the right shows the temperature profile (red) as a function of altitude for the The U.S. Standard Atmosphere (1976), a hypothetical model for the vertical distribution of atmospheric properties approximating mid-latitude conditions throughout the year. “The model is empirical, being based upon temperature measurements by radiosondes, rocketsondes, rockets and satellites and is defined in terms of a temperature profile extending from -5 to 1000 km. This profile is chosen so that the vertical profiles of pressure, density and composition, derived using one-dimensional physical equations, and the temperatures provide a best fit to the experimental data for the defined standard conditions” (AAIA, 2010). In this model, the temperature at altitudes of 47 to 51 km is 271K and the temperature is greater than 255K at altitudes of 41.4 to 56.5 km. Given that the thermal profile varies with time of day, day of the year, and strongly with latitude, this is remarkable agreement between a simple model of energy balance and a simple model of a complex and always changing atmosphere.

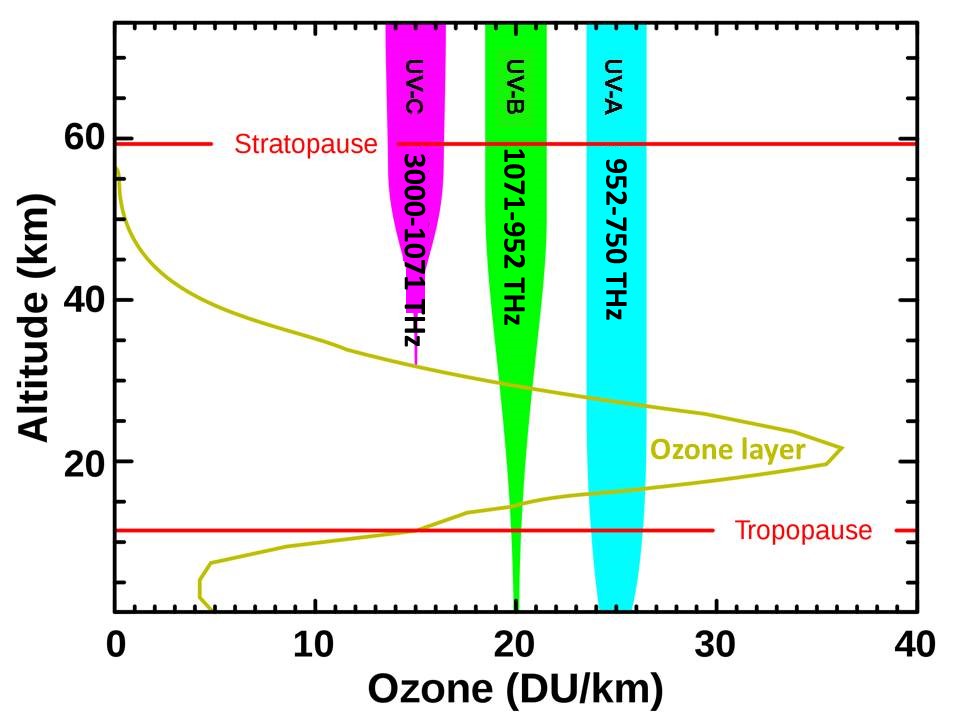
Earth’s surface loses thermal energy primarily through convection, what we experience as wind, storms, and weather. Convection establishes the lapse rate, the rate that temperature decreases with increasing altitude in the troposphere. The lapse rate averages 6.4^oC/km but varies from 5.5^oC/km in a wet atmosphere to 10^oC/km in dry air. The tropopause is the boundary between the troposphere heated from below by a sun-warmed Earth and the stratosphere heated from above by solar ultraviolet radiation. The highest energy ultraviolet radiation is absorbed high in the atmosphere with lower and lower energy radiation penetrating to lower and lower altitudes where it photodissociates oxygen (O₂) to cause the primary heating of the stratosphere. The stratopause is the altitude where the heating from below including heat from the tropopause and from photochemistry in the stratosphere, given all the details of atmospheric chemistry and physics, has the maximum warming and forms the radiative surface of the Earth-atmosphere system.

Above the stratopause, temperatures in the The U.S. Standard Atmosphere (1976) model fall to 187K at the mesopause between altitudes of 86 to 91 km and then start increasing in the thermosphere and exosphere to 1000K at 1000 km. But above the mesosphere, gas molecules are so far apart that temperature as defined by the kinetic theory of gases ceases to have much meaning. Furthermore, heat is not fed from below to support any radiative surface above the stratopause.

Note above that I have not mentioned greenhouse gases. They absorb infrared energy radiated from Earth up through the troposphere. But the vast majority of energy leaving Earth travels by convection up through the troposphere. Thus, greenhouse gases have little to no effect on the thermal energy balance of Earth.

Temperature versus volume

The primary macroscopic effect of temperature is to increase the volume of matter. This is how a mercury-in-glass thermometer works. Increasing the temperature of matter using a stove, for example, increases the frequencies and amounts of oscillation, lengthening the atomic and molecular bonds, and thereby increasing the volume. Increasing the frequencies and amounts of oscillation through absorption of radiation similarly increases the frequency and spectral amount of oscillations of the bonds, causing them to become longer, and thereby increasing the volume of matter. Heat dissipates over time; matter cools, shrinks, and becomes more dense. When temperature approaches absolute zero, the amount of oscillation approaches zero, and the volume becomes smallest, reaching its maximum density. Raise the temperature (the kinetic energy of oscillation) high enough, the bonds lose their shear strength, forming a fluid. Continue to raise the temperature and all bonds holding the molecules together come apart forming a gas. For a gas the bonds are reduced to collisions and perceptible temperature becomes proportional to the number of collisions per second, which according to the kinetic theory of gases and the ideal gas law, is proportional to the average velocity (kinetic energy of translation) of all particles. Raise the temperature of a molecule even higher and the molecular bonds come apart typically through photodissociaton and then photoionization. Raise the temperature of an atom even higher and the atomic bonds come apart. Frequency and spectral amount of oscillation of chemical bonds, volume of matter, and temperature of matter are all closely linked.

Radiant energy and the Universe

The discussion above of radiant energy leads to some rather provocative implications that extend beyond issues of climate. I mention them here to stimulate your thoughts.

Based on observations of the cosmic microwave background by the Planck spacecraft and the standard model of cosmology, the total mass-energy of the universe is thought to contain 4.9% ordinary matter, 26.8% dark matter, and 68.3% dark energy. Dark matter cannot be seen; it does not appear to reflect, absorb, or emit electromagnetic radiation but is inferred to exist because of its gravitational effects on ordinary matter. Dark energy is a hypothetical form of energy that permeates space and is thought to accelerate the expansion of the universe but is not seen. Many explanations have been proposed for these invisible forms of matter and energy as explained on the hyperlinks above and by other sources such as (Guth, 1998), (Carroll, 2007), and (Chaisson, and McMillan, 2011). I stated above that because Earth receives less than 5×10^-8 % of Sun’s radiation, there must be a lot of dark energy in our solar system that changes in time primarily as the rate of conversion of mass to energy in the Sun. I also showed that when matter cools to temperatures close to absolute zero, it only radiates and therefore only absorbs energy in the far infrared and microwave bands and that much higher frequencies in the near infrared, visible, ultraviolet wavelengths would pass straight through, making the matter invisible or dark. The map of the cosmic microwave background could therefore be the map of dark matter. The fact that matter shrinks as it cools and that our solar system and our galaxy, the Milky Way, is cooling and therefore shrinking, raises the possibility that the universe is not expanding but our domain of the universe is contracting, an alternative way to explain the observed red shift of distant light sources. All of these inferences need to be tested against observations.

Planck’s law says that bodies of mass radiate a broad spectrum of electromagnetic radiation most directly explained as reflecting the broad range of frequencies of oscillation of the molecular bonds. But given that the radiant surfaces of the sun and Earth are layers of gas, one might expect the radiation to reflect the frequencies of oscillation of the gas molecules rather than a broad spectrum. This raises the possibility that energy in space has a narrow spectrum of frequencies that causes a broad Planck spectrum of frequencies when it interacts with matter, including the matter in our sensors on satellites and interplanetary probes.

Joseph Fourier pointed out in 1822 (page 1) that “heat [thermal energy], like gravity, penetrates every substance of the Universe; its rays occupy all parts of space.” As we explore the properties of radiant energy and heat, we might do well to consider the possibility that the Universe is simply one electromagnetic energy field that is continuous throughout all of space and all of matter but that varies with location from the electrostatic forces holding matter together and pushing matter apart, to what we think of as electrons that (de Broglie, 1929) suggested may simply be standing waves of energy, all the way to radiation from distant stars. We might think about this Universe as containing domains all at different stages in a cycle where energy is created from mass in stars, dissipated over time leaving very cold, dense matter, perhaps in black holes, that expands rapidly into stars and planets again.

Summary

The most important lessons from following the energy are that the energy of electromagnetic radiation is simply a function of frequency, not bandwidth, that the energy absorbed by ozone is 48 times more energetic than the energy typically absorbed by carbon dioxide, that the peak spectral radiance received from the Sun is 69 times the peak spectral radiance received from Earth, and that radiant ultraviolet energy causes photodissociation so that it is converted very efficiently to temperature while only a fraction of the radiant energy absorbed by carbon dioxide is converted to translational kinetic energy and thus to the temperature of air. There simply is not enough energy in play with greenhouse gases to explain global warming.

The ozone depletion theory of global warming, on the other hand, explains all the different observations related to warming quite directly. There is substantial energy in play. The most energetic solar radiation reaching Earth has ultraviolet to visible frequencies. Photodissociation of ozone in the lower stratosphere absorbs solar energy strongly in the vicinity of 310 nm. When ozone is depleted, more of this high-energy radiation that causes sunburn and skin cancer reaches Earth, cooling the stratosphere and warming primarily Earth’s ocean. It is Earth’s ocean that must be warmed to bring Earth out of an ice age. The amount of ozone in the atmosphere determines how much high-energy, solar, ultraviolet radiation is absorbed primarily in the lower stratosphere and how much will ultimately be absorbed by Earth