Thermal Energy Is Not Additive

Richard Feynman, one of the best known and most provocative physicists of the 20th century, wrote in his Lectures on Physics: “It is important to realize that in physics today, we have no knowledge of what energy is. We do not have a picture that energy comes in little blobs of a definite amount” that can be added together (Feynman et al., 1963) (p. 4-2). Feynman received the 1965 Nobel Prize in Physics for his contributions to the development of quantum electrodynamics, which is, essentially, the study of how radiation interacts with matter.

Yet today, throughout classical and modern physics, we calculate energy as if it did in fact “come in little blobs of a definite amount” that can be added together to yield increased energy in a system of interest. This is the basis of the radiative forcing approach to climate change and the integration of radiant energy as a function of wavelength or frequency. It is also the basis for quantum physics, which is based on the concept that energy is quantized, i.e. that it only “comes in little blobs of a definite amount.” If a photon has a certain energy (E), most scientists conclude that 20 photons have 20 times as much energy (20*E). While it may be correct to think of 20 photons as having 20 times the capacity for containing energy (E) as one photon does, the energy (E) of each photon and of the ensemble of photons always remains the same no matter how many photons with that energy you have, because thermal energy is not additive.

The quickest way to get into a heated argument with any physicist or climatologist is to assert that the energy of two identical photons is not twice the energy of one of them. Nevertheless, energy is not additive, and recognizing that fact leads to transformative insights in climate science, quantum physics, and many other scientific fields. Transformations in science are rarely well received or easily understood at first, but the new insights they reveal can help to solve some major problems in physics.

A Simple Example

Temperature (T) is a physical property of matter that is an indicator of how much thermal energy is contained in a body of matter, whether solid, liquid, or gas. If you divide that body in half, you will have two bodies with the same temperature (T). If you then combine the two bodies again before either can lose heat, you will once again have a single body with temperature (T). Temperature is an intensive physical property of matter, meaning that the numerical value (magnitude) of temperature (T) is independent of the size of the system. An extensive physical property, on the other hand, in which the magnitude depends on the size of the system and is therefore additive for subsystems, is distinctly different. An example of an extensive physical property is mass. When you add masses together, you end up with more mass.

If you have two bodies at different temperatures T1 and T2, and you put them together in thermal contact and let them reach thermal equilibrium without losing heat to the surroundings, the new body will not have a temperature that is the sum of the two temperatures (T1 + T2); it will have a temperature somewhere between T1 and T2. If the bodies are of identical size and material, the new body will have a temperature equal to (T1 + T2)/2, the average temperature of the two bodies. Temperature results from microscopic oscillations of chemical bonds permeating the whole body. This is why temperature is an intensive physical property of matter that is not additive.

Energy

Feynman further states “there is a certain quantity, which we call energy, that does not change in the manifold changes which nature undergoes. … There is a numerical quantity which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number [energy] and when we finish watching nature go through her tricks and calculate the number again, it is the same” (p. 4-1). Energy changes in form, but does not change in quantity. This is known as the law of conservation of energy, one of the most basic laws of physics, to which there are no known exceptions.

Jennifer (Coopersmith, 2010)(p. 350), in her book Energy, the Subtle Concept, concludes that energy is “what makes things happen.” Energy is “the ‘go’ of the Universe.” Energy causes things to happen around us. No change is possible without allowing energy in some form to change into a different form. Energy essentially adds the dimension of time—if nothing changed, it would be impossible to tell, or quantify, time.

E = hν

In photochemistry and in quantum mechanics, energy (E) is defined by the Planck-Einstein relation as the Planck constant (h) times frequency ν (the Greek letter nu), i.e., E=hν, which is commonly thought of as the energy of a photon. According to this widely accepted equation, the energy of ultraviolet-B radiation, with a frequency of around 967 terahertz (commonly specified as a wavelength of 310 nanometers), is 48 times greater than the energy of the infrared radiation that is absorbed most strongly by carbon dioxide, which has a frequency of around 20 terahertz (14,900 nanometers). Nonetheless, climate models calculate that there is more energy (spectral radiance) in infrared than in ultraviolet-B because the bandwidth of infrared radiation that is absorbed by carbon dioxide is greater than the bandwidth of increased ultraviolet-B radiation that reaches Earth’s surface when ozone is depleted. This is simply another way of saying that there are more photons in the infrared than in ultraviolet-B, but, as noted above, this is irrelevant, because the energy in photons is not additive.

E=hν says that energy is only a function of frequency and that energy is not a function of the number of photons, of bandwidth, or of the amplitude of oscillation. It simply says that energy is frequency times a scaling factor, which means that low frequency is low energy, that high frequency is high energy, and that by setting ν equal to one, it is clear that Planck’s constant (h) is the energy “contained” in one cycle per second with units of joules per cycle per second, which resolves to joule seconds per cycle.

In dimensional analysis, it has become customary, especially since the organization of the International System of Units in 1960, to omit the word cycle, specifying the units of h simply as joule seconds. A joule, however, is defined as the energy transferred, the work done, when a force of one newton acts on an object in the direction of its motion through a distance of one meter. Linear distance is central to the definition of a joule. When thinking about energy in a cyclical process, it is important to recognize that the length of a bond between two atoms, for example, “travels” a linear distance from fully compressed to fully extended and then travels the same linear distance in reverse from fully extended to fully compressed. Thus in one cycle, the bond length “travels” a linear distance of twice the difference between fully extended and fully compressed, but the net physical distance travelled is zero. The word cycle describes distance travelled that is inherent in the definition of a joule. Omitting the word cycle omits the unit of distance required in the definition of energy. We have lived somewhat comfortably with omission of the word cycle because most scientists assume the word cycle when they use units of reciprocal second or hertz. It would be more precise and more physical to retain the unit of cycle so that we understand more clearly why energy (E) of a cyclical process is defined as cycles per second (ν) scaled by the Planck constant (h) and why energy is not a function of amplitude of oscillation in a frictionless atomic oscillator.

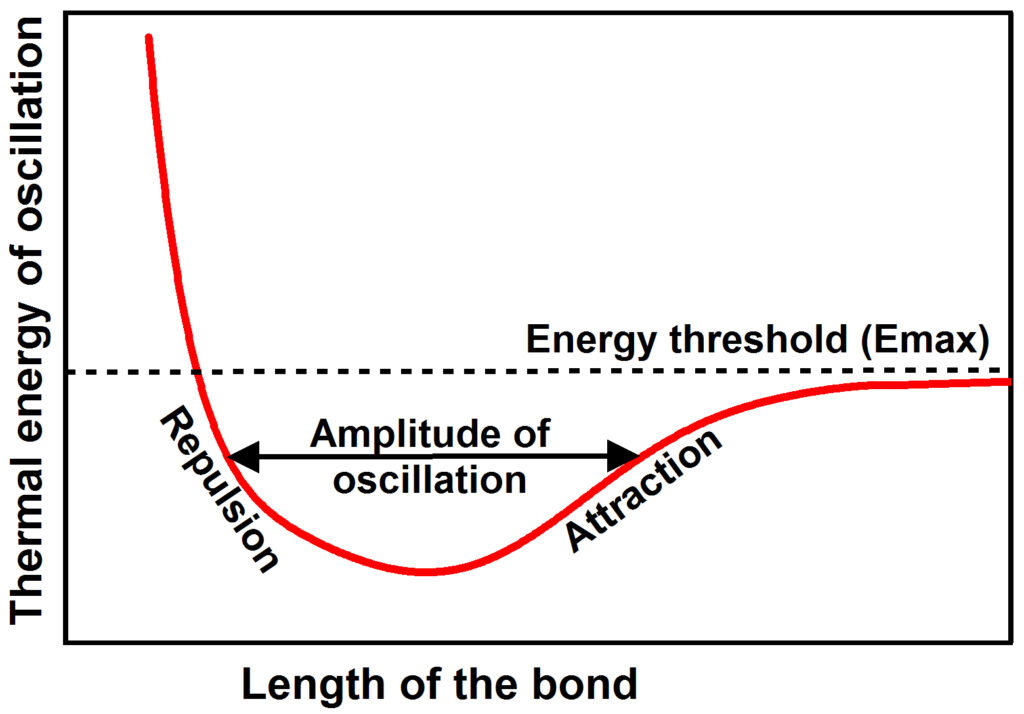
Thermal energy

The chemical bonds that hold atoms together to form matter are not rigid. They are observed to oscillate about an energy minimum between electrodynamic repulsive forces pushing the atoms apart and electrodynamic attractive forces pulling the atoms together. As the thermal energy of oscillation increases, the amplitude of oscillation increases until at some energy threshold (Emax) the bond comes apart. Energy (frequency) may increase in discrete steps as higher and higher normal modes (frequencies) of oscillation are activated. One such anharmonic atomic oscillator exists for every normal mode of oscillation of every degree of freedom of every bond in matter. Each oscillator has a characteristic resonant frequency and an amplitude of oscillation, the latter of which increases with increasing temperature (thermal energy). Because the oscillator is asymmetric, the average length of the bond increases with increasing thermal energy so that the volume of the matter expands with increasing temperature, something that is well observed.

An atomic oscillator of this type is asymmetric (anharmonic) because the force of repulsion increases very rapidly as like charges are pressed together whereas the force of attraction decreases much more slowly with distance as opposite charges separate.

An atomic oscillator of this type is frictionless and thus can oscillate for a very long time. The only way to add energy to such an oscillator, or to subtract energy from it, is through resonance. When the amplitude of oscillation at a specific frequency of one bond is larger than the amplitude of oscillation at the same frequency of an adjacent bond, the bond with the larger amplitude will “give up” energy to the bond with the lower amplitude until the amplitudes for both bonds are equal. The rate of energy transfer increases with increasing difference in amplitudes.

Heat

Heat consists of a very broad spectrum of frequencies of oscillation and is stored as bond oscillations, as is shown by the observation that the capacity of a material to store heat (the heat capacity) increases with the number of degrees of freedom of the bonds involved.

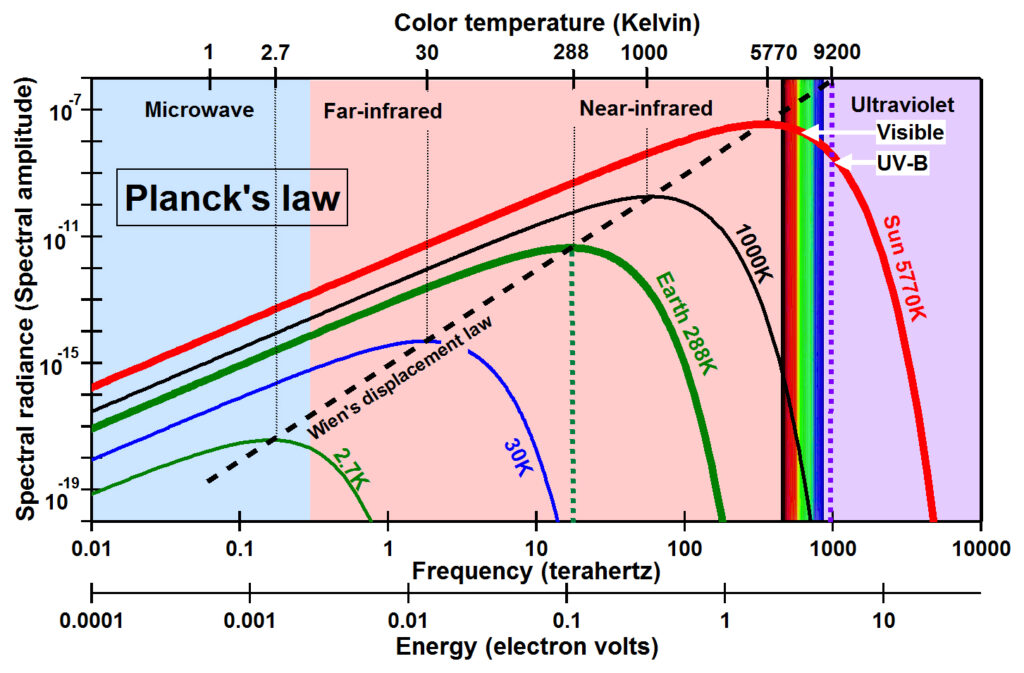
Max Planck (1914) proposed an empirical equation in 1900, now known as Planck’s law, describing, as a function of temperature, the observed spectral radiance emitted by a perfectly radiating and perfectly absorbing body of matter (a so-called black body) that has reached thermal equilibrium. Note that for Earth, at a temperature of 288K (15oC), heat includes frequencies from less than one cycle per second to well over 1014 cycles per second.

The filament of an incandescent light bulb has a temperature of around 3300K, emitting a broad spectrum of radiation according to Planck’s law that we perceive as being very hot. A green light-emitting diode (LED), on the other hand, emits frequencies primarily between 545 and 577 terahertz, a narrow spectrum that takes much less power to create and that we perceive as being quite cool. What we perceive as heat is the result of oscillations over a very broad range of frequencies. The amplitude of oscillation at each frequency may vary in many ways, but once thermal equilibrium is reached through conduction, the distribution of amplitudes is described by the smooth curves calculated using Planck’s law.

Planck’s law must also describe the oscillations on the surface of matter, since it is those oscillations of electric charge that induce electromagnetic radiation. Thus, Planck’s law tells us that heat in matter consists of a very broad spectrum of frequencies, each oscillating with a natural amplitude of oscillation specified by Planck’s law. Throughout the process of conduction, therefore, the frequencies and amplitudes of oscillation are all redistributed within the receiving body until, at thermal equilibrium, they can be described by a Planck curve. Each such curve specifies, for a given black body temperature, the natural amplitude of oscillation on the surface of the body at each specific frequency.

The amplitude of oscillation decreases inversely with the square of distance travelled because the rays diverge in two dimensions perpendicular to the line of sight. A laser, on the other hand, increases the natural amplitude of oscillation over a very narrow range of frequencies, moving the amplitude closer to Emax. A laser also nearly eliminates divergence so that a laser beam loses little amplitude of oscillation with distance.

Planck’s law is an equation that was derived empirically in an effort to explain observations made in the late 19th century, and still made today, measuring the thermal effect of radiation on the piece of matter in the sensor, typically a thermopile or resistor. The physical properties of radiation, however, are frequency (color) and amplitude (commonly thought of as brightness or intensity). Ideally the y-axis should be amplitude and the x-axis frequency, which is energy because E=hν. The traditional way of plotting Planck’s law has energy (watts per square meter) on the y-axis as a function of wavelength on the x-axis, but wavelength is inversely proportional to frequency and is therefore a measure of energy. Plotting energy as a function of energy assumes that energy is additive, which, as we have seen, it is not.

Note that the Planck curves do not cross each other. To make a body of matter hotter, you must increase the amplitude at each and every frequency, and you must increase the frequency of the maximum amplitude, described by Wien’s displacement law. These are the reasons why heat flows by resonance from hot to cold and cannot flow by resonance from cold to hot. These are also the reasons why there is no flow of heat from a body at a given temperature to a body at the same temperature. In fact, thermal equilibrium is defined as the state where there is no net flow of heat. Thus, radiation from Earth cannot warm Earth, as is assumed by greenhouse-warming theory—radiation from Earth, even if it has not travelled any distance, contains the same amplitudes of oscillation and the same frequency for the maximum amplitude as oscillations on Earth’s surface. Once radiation has travelled any distance, it contains less amplitude of oscillation than the surface of the radiating body. Earth’s heat, therefore, cannot physically flow back to Earth.

Photons

Spectral physicists have documented experimentally, in extremely precise detail (Rothman et al., 2013), that a molecule of gas absorbs energy from an electromagnetic field along spectral lines whose frequencies are equal to the frequencies of the normal modes of oscillation of all the degrees of freedom of all the bonds that hold the molecule together. In other words, the amplitudes and frequencies of oscillation in the electromagnetic field cause resonance of the normal modes of oscillation of the absorbing molecule, transferring energy to the molecule at those frequencies where the amplitudes are greater in the field or transferring energy from the molecule to the field where the amplitudes are greater in the molecule. If we think of the packet of energy transferred as being a photon, then the frequency content (energy content) of the photon is determined by the molecule in the immediate vicinity of the molecule. The photon, therefore, could not have traveled from Sun or from any other radiating body. If it had, there would have to be different photons for each chemical species that absorbs radiation, a highly improbable circumstance.

Also, electromagnetic radiation spreads out with the square of distance. If the electromagnetic field were quantized into photons at its source, it is impossible to pack those photons closely enough as they leave a distant star to appear continuous to an observer on Earth. While the photon concept is extremely useful mathematically and is a cornerstone of quantum mechanics, it is not clear that photons traveling from a radiating body physically exist. What is clear is that electromagnetic radiation is a frequency field, continuous in three dimensions, which can be measured and mapped out with an appropriate sensor. Disturbances appear to travel through this field at the velocity of light, which, according to Maxwell (1865), is equal to one over the square root of the product of electric permittivity times magnetic permeability, which is proportional to the time it takes for an electric field to induce a magnetic field, and for the magnetic field to then induce an electric field (one cycle) leading to a self-sustaining process. In other words, the velocity of light is proportional to the smallest increment of time at which radiation can propagate.

What is Electromagnetic Radiation?

Electromagnetic radiation transfers heat through air and space from a warmer body of matter to a colder body of matter. Heat consists of a broad spectral range of frequencies, as described by Planck’s law. What is most peculiar about radiation in air and space is that these frequencies do not interact with each other. While their amplitudes (intensities) decrease inversely with the square of increasing distance, the frequencies do not change, even over galactic distances, except for Doppler effects. In matter, amplitudes and frequencies interact with each other across the bonds that hold the matter together. A seismic wave, for example, can be approximated by a Fourier series, an infinite series of terms that are proportional to a frequency times an amplitude and are added together. Radiation in space, on the other hand, contains all these frequencies and amplitudes, but there are no bonds across which they can interact. Radiation is, therefore, a Fourier series without plus signs—in other words, it is simply a coexistence of a broad range of non-interacting frequencies.

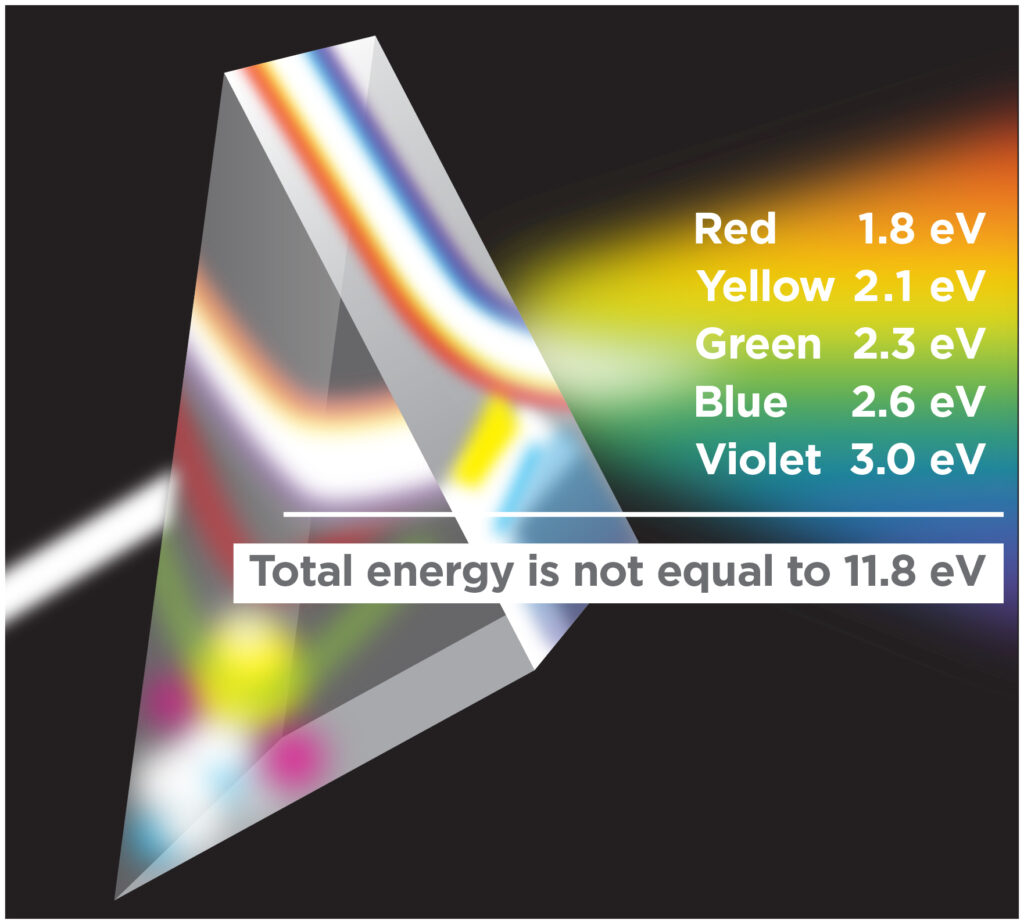
White light, for example, consists of a spectrum of frequencies many of which we see when they interact with matter, such as in a rainbow or when passed through a prism. The energy at each frequency is equal to E=hν. It does not make physical sense to add frequencies, and thus it does not make physical sense to add energies. You cannot add up selected frequencies or energies from the visible spectrum to yield a frequency or energy in the ultraviolet range. Green light, at 560 terahertz, for example, cannot be added to blue light, at 630 terahertz, to yield ultraviolet-C radiation at 1190 terahertz. Frequency and energy are intensive physical properties that are not additive.

What Is Quantized?

Frequency in Nature is a continuum extending over dozens of orders of magnitude from radio signals to gamma rays. If E=hν, then energy is also a continuum and is therefore not itself quantized, but the effects of energy are often quantized by the absorbing matter. When a molecule of gas absorbs energy from an electromagnetic field along spectral lines, each spectral line represents a quantum of energy. Each spectral line is slightly broadened, having some finite width containing a narrow continuum of frequencies and therefore a narrow continuum of energies. Hence we can think of a spectral line as a quantum.

Einstein (1905) introduced the concept of light quanta to explain the photoelectric effect, in which certain frequencies of light cause electrons to be released from certain polished metal surfaces. Electrons are only emitted when the frequency (energy) of the light exceeds some threshold frequency (with an energy of Emax), typically in the blue to violet range. Similar threshold effects hold for most chemical reactions. Visible light can power photosynthesis, whereas infrared radiation does not have high enough frequencies, does not contain high enough energies, to do that. When a molecule of oxygen (O2) absorbs frequencies in the vicinity of 1236.77 terahertz, the molecule is dissociated into two atoms of oxygen (2O). The energy of this frequency (5.11 electron volts or 8.19 x 10-19 joules) is sufficient to cause dissociation. Similar threshold energies apply to electronic transitions and to ionization. To have an effect, radiant energy must contain sufficiently high frequencies (energies). Thus, the effects of energy on matter are quantized, while energy itself is a continuum.

Spooky Action At a Distance

Every molecule of everything that we can see, is oscillating primarily at some frequency (color) with some amplitude (brightness). When we look in the direction of that molecule with clear line of sight, the oscillations of that molecule cause three different types of cones in our eyes to resonate. Each type of cone is most responsive to a narrow band of frequencies often referred to as red, green, or blue bands. Our brains then turn the responses of these three types of cones into our perception of the color of that molecule. Our eyes are most responsive to the visible spectrum of frequencies because the size of cells in our body making up the cones resonate best within these narrow ranges of frequencies. Ultraviolet radiation can damage the receptor cells, so our eyes have adapted by making the lens impervious to ultraviolet light. Furthermore, most ultraviolet radiation from Sun is filtered out by the atmosphere. The CMOS sensor of a digital camera similarly encodes levels of red, green, and blue that a printer or computer monitor reproduces as a pixel at one specific color (frequency).

The observation that oscillations of a molecule over there cause similar oscillations of cells in the cones of our eyes over here, without anything visible connecting the molecule to the cells, is what Albert Einstein called “spooky action at a distance.” In quantum mechanics, this is known as quantum entanglement, which has taken on a rich set of mathematical concepts that may obfuscate the simple possibility that radiation “propagates” by resonance. Oscillations on the surface of the antenna of a radio transmitter are received by a radio receiver tuned to resonate at that precise frequency. A molecule similarly oscillates at a specific color that causes any appropriate sensor within line of sight to resonate at the same frequency. This is why a crowd of people all observe more or less the same thing when they are looking in the same direction. Heat, on the other hand, is radiated by causing resonance over a very broad band of frequencies described by Planck’s law. What travels through space is oscillations with a specific amplitude at each frequency. You cannot see these oscillations until they interact with matter and anything in the line of sight, such as gas molecules, pollution, or clouds, will reduce the amplitude of oscillation at any frequency with which it resonates. We think of oscillations of charge on the surface of matter, as inducing an electric “field” that induces a perpendicular magnetic field, that induces a perpendicular electric “field,” and so on in a self-sustaining way, delivering frequency and amplitude of oscillation to any matter within line of sight. Now that we recognize the primary role of resonance, we may wish to revisit the mathematics of what light is and how it “travels.”